Evidence base
Explore an overview of contemporary research and numeracy practice in Australia.
Defining numeracy
In Australia, educators and policy makers have embraced a broad interpretation of numeracy similar to the Organisation for Economic Co-operation and Development [OECD] definition of mathematical literacy (Goos, Geiger, & Dole, 2012).
The Australian Association of Mathematics Teachers [AAMT] (DEETYA, 1997, p. 15) stated that:
To be numerate is to use mathematics effectively to meet the general demands of life at home, in paid work, and for participation in community and civic life.
This definition has become widely accepted in Australia and has formed the basis for much numeracy-related research and curriculum development.
The Victorian Curriculum and Assessment Authority expanded upon the AAMT definition:
Numeracy is the knowledge, skills, behaviours and dispositions that students need in order to use mathematics in a wide range of situations.
Numeracy involves recognising and understanding the role of mathematics in the world and having the dispositions and capacities to use mathematical knowledge and skills purposefully.
Number, measurement and geometry, statistics and probability are common aspects of most people’s mathematical experience in everyday personal, study and work situations.
Equally important are the essential roles that algebra, functions and relations, logic, mathematical structure and working mathematically play in people’s understanding of the natural and human worlds, and the interaction between them.
Children and young people are exposed to increasingly sophisticated and refined mathematical understanding, fluency, problem-solving, and reasoning. These proficiencies enable students to respond to familiar and unfamiliar situations by employing mathematics to make informed decisions and solve problems efficiently (VCAA, 2017).
There is now strong evidence that other areas of development – such as resilience and perseverance – support achievement in numeracy as well.
Although definitions of numeracy vary, it is broadly accepted that being numerate extends beyond the mastery of basic arithmetic skills (Goos, Geiger, Dole, Forgasz, & Bennison, 2019).
Being numerate involves the capacity to make sense of non-mathematical contexts through a mathematical lens and solve real-world problems (Geiger, et al., 2015). Essentially it is the “ability to use, apply, interpret, and communicate mathematical information and ideas” (OECD, 2016, p. 75).
According to AAMT, in school settings, numeracy is a fundamental component of learning, performance, discourse and critique across all areas of the curriculum. It involves the disposition to use, in context, a combination of:
- Underpinning mathematical concepts and skills from across the discipline (numerical, spatial, graphical, statistical and algebraic)
- Mathematical thinking and strategies
- General thinking skills
- Grounded appreciation of context (DEETYA, p. 15).
Goos (2007), however, argued that a description of numeracy for the 21st century needs to better recognise the rapidly evolving nature of knowledge, work, and technology. It is vital for critical citizenship, including the ability to question ways in which data are used for constructing arguments to inform, persuade or shape decision-making (Goos, et al., 2019). A model for Numeracy in the twenty-first century represents the multifaceted nature of numeracy and was intended to be used as an instrument for planning and reflection (Goos, Dole, & Geiger, 2012). The model is discussed further in the Numeracy in the
In school settings, numeracy is a cross-curricular issue and in
In early childhood settings, numeracy is enriched through young children developing their knowledge and skills in mathematics while applying them to their own contexts (Perry, 2000).
Numeracy, the application of mathematics to a contextual problem or challenge, can be enacted through play in prior-to-school settings, home, shopping centres and schools (Perry, 2000). See Numeracy across the curriculum in the Numeracy in the
Numeracy within an international context
The term numeracy is commonly used in countries such as Australia, New Zealand, UK, Canada, and, South Africa while the USA, for example, uses terms such as quantitative literacy or mathematical literacy to describe numeracy.
Furthermore, other expressions, such as statistical and financial literacy (Sawatzki, 2017), are used to denote more
In the UK, the term numeracy was first coined in 1959 in the Crowther Report where it was referred to as the ‘mirror image of literacy’ (Crowther, 1959, par. 398).
According to the Cockcroft Report (Cockcroft, 1982), numeracy implies an ‘at-homeness’ with numbers and an ability to make use of mathematical skills which enable an individual to cope with the practical demands of everyday life.
Numeracy involves more than being able to manipulate numbers; Johnston (1994) likened it to a ‘bridge between mathematics and the real world’ (p. 34).
In Askew et al.’s (1997) Effective Teachers of Numeracy study, the authors defined numeracy as “the ability to process, communicate and interpret numerical information in a variety of contexts” (p. 7). In this regard, numeracy has a more narrow meaning than the one that is used in the Victorian context. The terms quantitative literacy, mathematical literacy (O’Donoghue, 2002) and number sense (Howden, 1989; McIntosh, Reys & Reys, 1992) have all been used to describe what is essentially understood as ‘numeracy’.
Reflective Prompt
How do you define numeracy?
Why is it important to have an agreed understanding of numeracy?
Reflective Prompt
How do you define numeracy?
Why is it important to have an agreed understanding of numeracy?
Connecting numeracy and mathematics
In a recent synthesis of numeracy literature, Geiger et al., (2015) outlined the development of the concept of numeracy internationally and presented research on numeracy practice. The article highlights the challenges associated with agreeing on a widely accepted definition for numeracy and how to best promote the development of numeracy capabilities.
Numeracy and mathematics are not synonymous (DEETYA, 1997), and although the terms numeracy, mathematics and mathematical literacy often appear to be used interchangeably (Groves et al., 2006), the term numeracy has been useful in highlighting the importance of developing students’ abilities to use school mathematics outside of educational settings.
The definitions of numeracy presented earlier all include reference to numeracy being about using mathematical ways of thinking and
The implemented mathematics curriculum underpins numeracy, but mathematics in educational settings includes learning mathematics as a discipline (DEETYA, 1997).
Students are helped to become numerate (able to use their mathematics) in different contexts through a range of experiences outside of their learning of mathematics (Morony & Brinkworth, 2003).
Reflective Prompt
Look at the following Venn diagrams showing different representations of the relationship between numeracy and mathematics.
Which diagram do you most relate to and why?
How else could you represent the relationship between numeracy and mathematics?
Reflective Prompt
Look at the following Venn diagrams showing different representations of the relationship between numeracy and mathematics.
Which diagram do you most relate to and why?
How else could you represent the relationship between numeracy and mathematics?
A numerate person, therefore, has the ability to use and apply mathematics in a range of contexts outside the mathematics classroom.
Mathematics is learned as a body of knowledge, which can then be applied to a context through determining that ‘some mathematics will help here’ (Perso, 2011, p. 32).
Although mathematics does involve a body of knowledge, the Victorian Curriculum (VCAA, 2017), extended mathematics to include the proficiencies of understanding, fluency, problem-solving, and reasoning.
Reflective Prompt
Can you be numerate without having a good conceptual understanding of mathematics?
Reflective Prompt
Look at the following Venn diagrams showing different representations of the relationship between numeracy and mathematics.
Which diagram do you most relate to and why?
How else could you represent the relationship between numeracy and mathematics?
Not all mathematics that is taught in schools, therefore, is akin to numeracy.
Perso offered the following example of a task that assesses a mathematical skill, rather than an application of
Use the Pythagorean Theorem to find the height of a tree which casts a shadow 2.35 metres long and has an angle of elevation with the ground of 53 degrees (give your answer to two decimal places)
Similarly, a typical primary textbook problem might ask students to:
Measure these angles using a protractor.
In this example, while the students may be applying
Reflective Prompt
How might you design a task to assess numeracy?
What would this look like?
Reflective Prompt
How might you design a task to assess numeracy?
What would this look like?
For further examples of the distinction between mathematics and numeracy, see Assessing Numeracy and NAPLAN (Perso, 2011).
For examples of tasks that develop numeracy, see Professor Peter Liljedahl article – Numeracy task design: a case of changing mathematics teaching practice.
Watch Professor Robyn Jorgensen provide a clear distinction between mathematics and numeracy in the following presentation.
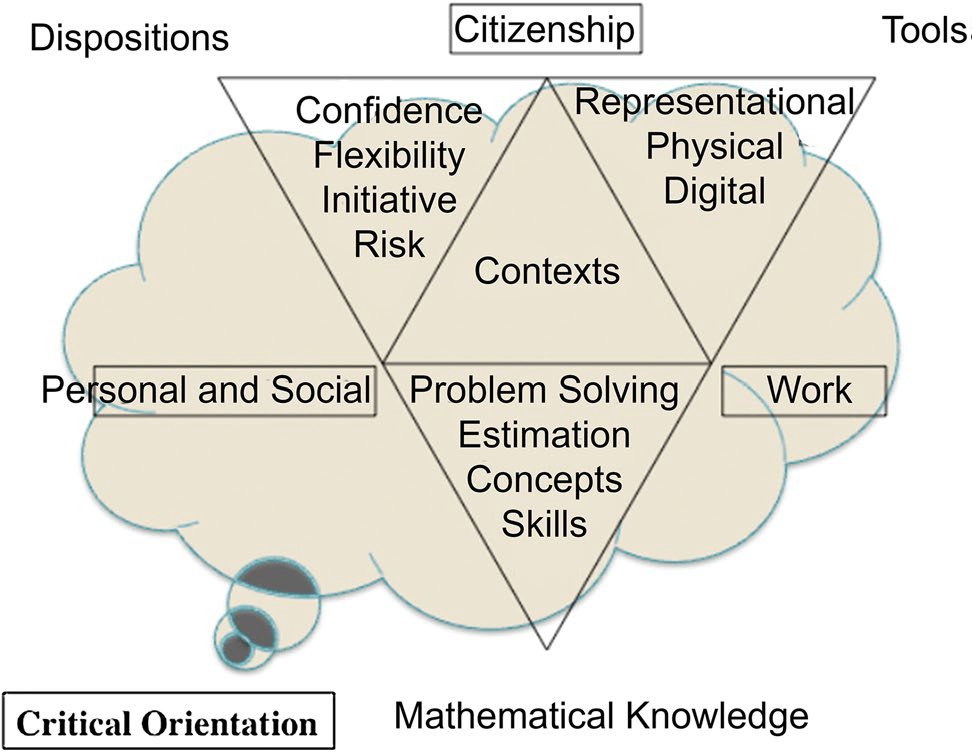
Numeracy in the twenty-first century
To represent the multi-faceted nature of numeracy in the twenty-first century, in 2007 Professor Merrilyn Goos developed a model for numeracy in the 21st century (see below) which contained a number of elements related to numeracy knowledge and behaviours.
These elements were described as:
Mathematical Knowledge: Mathematical concepts and skills; problem-solving strategies; estimation capacities.
The table below provides a description of the elements of the numeracy model (Goos, Geiger, & Dole, 2012).
Other frameworks for interpreting numeracy are documented in the literature. For example, the Numeracy Framework developed by Willis and Hogan (Hogan, 2000) incorporated three types of knowledge:
- Mathematical knowledge – the knowledge needed for intelligent mathematical action
- Contextual knowledge – the ability to link mathematics to experiences
- Strategic knowledge – the ability to ask questions about the application of particular mathematical knowledge
Reflective Prompt
Can you think of questions or experiences that would help students develop these different forms of knowledge?
Does mathematics always have to include a context to develop numeracy?
Reflective Prompt
Can you think of questions or experiences that would help students develop these different forms of knowledge?
Does mathematics always have to include a context to develop numeracy?
Critical numeracy
Critical numeracy (Watson, 2009) uses a similar model to the Four Resource Model of Critical Literacy (Luke & Freebody, 1990) to build students’ capacities to ask questions about the meaning, validity and usefulness of texts containing mathematical concepts or information.
By using a similar model to critical literacy, students can recruit and build on the visible thinking strategies that they are developing whether in a literacy or numeracy context.
Visit this site Tasmanian Department of Education page on critical numeracy to discover more about this model and to access a video of Jane Watson talking about critical numeracy.
Reflective Prompt
How is critical numeracy similar and different to the VCAA definition of numeracy?
Reflective Prompt
How is critical numeracy similar and different to the VCAA definition of numeracy?
These frameworks, the Numeracy Learning Progressions and supporting research has informed the development of the Numeracy Focus Areas.
Read more about the formation and teaching of the six Numeracy Focus Areas across the three developmental stages.
Numeracy across the curriculum
A numerate person is defined as someone who has the ability to use and apply mathematics in a range of contexts outside educational settings.
In educational settings, this ability can be developed through cross-curricular activities.
The Numeracy in the Learning Areas Project, funded by the South Australian Department of Education and Children’s Services, offered example case studies. These case studies
Health and Physical Education with Year 8 students (Peters et al., 2012)
Students carried out activities such as investigating a scaled-up life-size version of a Barbie doll to determine and compare the body proportions to an adult
The role of numeracy was further developed through investigating media coverage of sports, and students compared the unequal space devoted to male and female sports.
The students investigated their physical activity during a typical week using a pedometer.
Numeracy in society and environment with Year 7 students (Cooper et al., 2012)
In this case study, the students visited local war memorials. They focused on time, continuity and change as they researched the military record of a soldier.
Students used
Numeracy and English with Year 8/9 students (Willis et al., 2012)
In this case study, the students researched the best path for a new expressway to be built in their local area. The task involved managing constraints and keeping to a budget.
In these three case studies, the students were involved in authentic activities that made use of real-life information, giving them
Mathematics was given a numeracy context to explore the curriculum subjects in depth and they were encouraged to develop a critical orientation as they made judgements about the accuracy and reasonableness of their solutions. As one teacher said:
“One of my favourite catch phrases that I borrowed from the researchers was the ‘critical eye’ idea. They helped me to give a title to what I was trying to instil in the students… and the ability to look at something and think, ‘Is that what I was expecting? Does it look or feel right?’” (Willis et al., 2012 p. 15)
Further case studies of numeracy across the curriculum are presented by Geiger, Forgasz, and Goos (2015).
These studies indicated the use of critical numeracy with a focus on reasoning and critical examination of data with secondary students.
Social education lesson with Year 9 students:
Students, about to go on a school trip to Vietnam, practised bargaining at a market place and converting between Australian dollars and Vietnamese dong (conversion rate is typically 1 AUD = 17000 VND).
This required the students to carry out calculations with large numbers quickly and mentally in an authentic context.
English lesson with Year 7 students:
In this case study, students investigated how mass media uses data to inform and/or manipulate opinion.
The students were asked to examine surveys presented in newspaper articles about parents’ views on homework and on dog attacks. Students wrote an opinion piece that required them to research further the data.
In both case
Sellars (2017) investigated how numeracy across the curriculum could encourage students in primary schools to think more critically about the mathematical tools and concepts they were using and to make connections.
Sellars’ recent edited book (2018) explores numeracy across a range of non-mathematical subject areas, such as dance, drama, history, health, science, physical education, music and the visual arts.
The range of contexts
Numeracy and the proficiencies
It is acknowledged that the mathematics used to support numeracy is learned through a body of knowledge and the proficiencies.
The Australian Curriculum Assessment and Reporting Authority (2017) has outline four proficiencies as Understanding, Fluency, Problem-solving and Reasoning and the Victorian Curriculum: Mathematics, Foundation-10, (VCAA, 2017) has further defined these.
These proficiencies are the actions students engage in when learning mathematics and working mathematically, but what is less clear is how these proficiencies relate to learning
Numeracy and understanding
“The will and the skill are certainly necessary conditions for solving problems, but are they sufficient?” (Hurst, 2018)
Understanding is defined as making connections between representations of numbers and having concepts of partitioning and combining numbers (VCAA, 2017).
Richard Skemp’s seminal writing from the 1970s explained the difference between instrumental knowledge (rules without reasons) and relational understanding (knowing both what to do and why).
Gould (2016) explained how issues arise when learning rules without reason. Rules can appear to change depending on the mathematics involved, particularly when the mathematics becomes more complex.
Take, for example, the errors students make in subtraction; the most common error is to subtract the smallest number from the largest, such as in the problem 96 – 58 to get the answer 42. These types of errors show students’ lack of understanding of subtraction.
If students hold a relational understanding of mathematics when carrying out computational procedures, they are less likely to make errors when applied to other numeracy contexts. For example, Hurst (2018) suggested using examples in context to encourage estimation.
I have $53 and I spend $27. How much money do I have left? Is the answer more than $30 or less than $30?
“It is important to determine how students solve mathematics problems. Not just whether they have relevant skills but also if they understand what they are doing. When students practice procedures, they do not understand there is a clear danger they will practice incorrect procedures.” (Hurst, p.19)
Hurst argued that the predominance of teaching computational procedures at the expense of concepts and connections limits students’ understanding and that there needs to be a focus on both the concepts and the procedures. It is not that learning one will necessarily develop the other, but that teaching
Reflective Prompt
Can you think of examples where students have made errors that suggest they are relying on “rules without reasons”?
Reflective Prompt
Can you think of examples where students have made errors that suggest they are relying on “rules without reasons”?
Fluency is defined as developing skills in choosing procedures and in recalling facts and concepts (VCAA, 2017). Research into fluency has helped us to question the extent to which the knowledge of facts
For example, Heirdsfield, Dole, and Beswick’s (2007),
The teaching experiment used in this
Key facts seemed to be facts to 10, facts through 10, and doubles. The study noted the importance of tailoring instruction to the needs of learners and the delicate balance between explicit instruction and encouraging students’ own thinking.
The use of procedural fluency
Reflective Prompt
How might you help students develop fluency in a way that can support numeracy?
Reflective Prompt
How might you help students develop fluency in a way that can support numeracy?
“In the real world…We have to make the judgments and decisions about what mathematical knowledge might be relevant, and how to apply that knowledge.” (Turner, 2011, p. 58)
Problem-solving is defined as formulating, modelling and recording authentic situations involving operations, comparing numbers and using properties of numbers to continue patterns (VCAA, 2017).
Problem-solving is about the application of mathematical knowledge and this includes application to contexts outside educational settings.
Turner (2011) suggested six competencies that are needed to apply mathematical knowledge to solving real-life problems. These were:
- Communication – reading and interpreting statements, then forming a mental model of the situation
- Mathematising – transforming the problem to a mathematical form using a known or given
mathematical model or by creating a model - Representation – translating between different representations (e.g. equations, formulas, graphs, diagrams and concrete materials) to understand the situation, find a solution process and present the solution
- Reasoning and argument – being able to explore how different pieces of information are connected in a problem and to provide justifications
- Devising strategies – finding a mathematical strategy to solve a problem
- Using symbolic formal and technical language – understanding and using symbolic expressions (e.g. arithmetic expressions and operations) and the formal, technical language needed to interpret the mathematics.
Reflective Prompt
What are some of the difficulties students experience in solving problems?
How do these difficulties relate to the six competencies that Turner has suggested?
Reflective Prompt
What are some of the difficulties students experience in solving problems?
How do these difficulties relate to the six competencies that Turner has suggested?
Reasoning plays a “critical role in developing students’ understanding and promoting creative thinking in mathematics” (Vale, Bragg, Widjaja, Herbert, & Loong, 2017, p.3)
Reasoning plays a “critical role in developing students’ understanding and promoting creative thinking in mathematics” (Vale, et al., 2017, p. 3).
Research has suggested that primary students have the potential to promote mathematical reasoning but that they often experience difficulties in working this way due to limited opportunities to justify or generalise (Clarke, Clarke, and Sullivan, 2012).
Further research has shown how primary students can engage in reasoning through the Magic V task (Bragg, Loong, Widjaja, Vale, & Herbert, 2015) and the Is it True? task (Bragg & Herbert, 2017).
A stumbling block in the teaching and learning of reasoning has been the limitation in understanding what reasoning is. Some Victorian teachers are unable to define reasoning and were
Whilst research has focused on mathematical reasoning, research into students’ use of reasoning in numeracy is lacking.
Reflective Prompt
How do you define reasoning?
How do you encourage your students’ reasoning in your classroom?
How might reasoning in mathematics support numeracy?
Reflective Prompt
How do you define reasoning?
How do you encourage your students’ reasoning in your classroom?
How might reasoning in mathematics support numeracy?
“…mathematics content is delivered through language and so all mathematics teachers are teachers of the language of mathematics” (Adoniou & Qing, 2014, p. 12)
We often think that mathematics is ‘language free’, but the demands of the mathematics curriculum often mean that students are working in two registers: everyday language and specialist mathematics language. Some terms have specific technical meanings in mathematics, e.g. ‘volume’ or ‘prime’ and others have a precise meaning such as ‘half’.
Working with these two language registers can create ambiguities and challenges for many students, particularly for students learning English as an Additional Language; they are learning two languages at the same time.
These challenges become more problematic when
Adoniou and Qing (2014) suggested that “…mathematics content is delivered through language and so all mathematics teachers are teachers of the language of mathematics” (p.12). As such, teachers have a responsibility to become more aware of the language ambiguities and the challenges students face when learning mathematics.
Adoniou and Qing analysed the language demands in a Year 10 mathematics textbook and identified some of the key language challenges such as word order and syntax, as well as the interpretation of symbols and visuals. They suggested strategies that can support students’ use of the mathematics language in textbooks:
- ordering instructions
- labelling diagrams
- matching word sentences and definitions with diagrams and symbols
- writing or providing verbal instructions for each other.
To learn more about the language to support the teaching of each numeracy focus go to the Numeracy Focus Area section, where examples of appropriate language
Reflective Prompt
Consider the language backgrounds of the learners in your context.
What strategies might you use to encourage and support their mathematical language development?
Reflective Prompt
Consider the language backgrounds of the learners in your context.
What strategies might you use to encourage and support their mathematical language development?
Reforms in teaching numeracy
Developing both a body of knowledge and developing proficiencies are seen to be important in learning
However, the relationship between understanding, fluency, reasoning and problem-solving has been questioned by some mathematics educators.
For example, Westwood (2011) suggested that students need to develop automaticity in recalling number facts and in applying computational
Westwood further contended that, even though the long-term goal might be to develop abilities in numeracy, direct instruction is needed to help students develop computational skills and knowledge of number facts, particularly if they are falling behind in their learning in mathematics.
This thinking has sometimes clashed with the approaches taken in many school settings in teaching numeracy.
As noted by American Educational Psychologists, Clark et al. (2012) in the US, some researchers are advocating that teachers give explicit guidance in how to carry out mathematical procedures, accompanied by practice and feedback. Clark et al. suggested that problems be introduced to practise the application of recently learnt content and skills, but that problems are not used for discovering the mathematical content and skills needed for numeracy.
These views raise concerns in more progressive researchers and mathematics educators, who fear that direct modelling of computational procedures for copy and practise may not help students develop an understanding of the mathematics involved
These non-traditional researchers and educators would argue that too much time is spent on doing written calculations, as opposed to the use of mental calculations to solve problems
Reflective Prompt
How can you be sure that all students will develop the necessary skills and knowledge for numeracy if you use a problem-based approach to teaching numeracy?
Would the teaching of standard algorithms support numeracy? Why or why not? See Clarke (2005) article
Reflective Prompt
How can you be sure that all students will develop the necessary skills and knowledge for numeracy if you use a problem-based approach to teaching numeracy?
Would the teaching of standard algorithms support numeracy? Why or why not? See Clarke (2005) article
Developing a capacity to teach numeracy
Effective teaching of numeracy
In their seminal study ‘Effective Teachers of Numeracy’, Askew et al. (1997) identified that what distinguished highly effective teachers from other teachers was a particular set of coherent beliefs which underpinned their teaching of numeracy.
They identified three sets of belief orientations which were:
- Connectionist: beliefs based around both valuing pupils’ methods and teaching strategies with an emphasis on establishing connections within mathematics;
- Transmission: beliefs based around the primacy of teaching and a view of mathematics as a collection of separate routines and procedures; and,
- Discovery: beliefs clustered around the primacy of learning and a view of mathematics as being discovered by pupils.
“… it was clear that those teachers with a strongly connectionist orientation were more likely to have classes that made greater gains over the two terms than those classes of teachers with strongly discovery or transmission orientations.” (Askew, et al., 1997, p. 28).
Teachers within each orientation held a particular set of beliefs about what it is to be a numerate pupil, how pupils learn to become numerate and how best to teach a pupil to become numerate.
In summary, Askew et al., (1997) found that highly effective teachers:
- Held a particular set of coherent beliefs and understandings which underpinned their teaching of numeracy, including what it means to be numerate, the relationship between teaching and pupils’ learning of numeracy, presentation and intervention strategies
- Used teaching approaches which connected different areas of mathematics and different ideas in the same area of mathematics using a variety of words, symbols and diagrams
- Used pupils’ descriptions of their methods and their reasoning to help establish connections and to address misconceptions;
Emphasised the importance of using mental, written, part-written or electronic methods of calculation and particularly emphasised the development of mental skills - Ensured that all pupils were being challenged, not just those who were considered
more able - Challenged pupils to think through explaining, listening and problem-solving
- Encouraged purposeful discussion
- Used a variety of different assessment and recording methods to monitor pupils’ progress
- Had knowledge and awareness of conceptual connections between the areas that they taught in the primary mathematics curriculum
- Were more likely to have undertaken mathematics-specific continuing professional development over an extended period
- Displayed very positive attitudes to mathematics.
Reflective Prompt
Access the Effective Teachers of Numeracy report.
Review the different belief orientations in Table 3.1 (pp. 35-36). Where would you situate yourself in relation to these beliefs?
Do you identify more with the connectionist, transmission or discovery beliefs?
What impact do your beliefs have on how you teach students to become numerate?
Reflective Prompt
Access the Effective Teachers of Numeracy report.
Review the different belief orientations in Table 3.1 (pp. 35-36). Where would you situate yourself in relation to these beliefs?
Do you identify more with the connectionist, transmission or discovery beliefs?
What impact do your beliefs have on how you teach students to become numerate?
Characteristics of effective teaching of numeracy
A comprehensive study undertaken in Victoria by Professor Doug Clarke and others (2002) identified a number of characteristics common to effective teaching of numeracy.
As part of the Early Numeracy Research Project, they found that effective teachers of numeracy in the early years:
- Focus on important mathematical ideas and make the mathematical focus clear to children
- Structure purposeful tasks that engage children and enable different possibilities, strategies and products to emerge
- Use a range of materials/representations/contexts for the same concept
- Use teachable moments as they occur and make connections to previous mathematical experiences
- Use an introductory whole group activity to engage children and then a variety of individual and group structures within the lesson
- Use a range of question types to probe and challenge children’s thinking and reasoning and encourage children to explain their mathematical thinking/ideas
- Have high but realistic expectations of all children
- Use reflection to draw out key mathematical ideas during and/or after the lesson
- Use a variety of assessment methods and modify planning as a result of assessment
- Display confidence in their own knowledge of mathematics at the level they are teaching and a belief that mathematics can and should be enjoyable.
Click here for a full copy of the Early Numeracy Research Project.
Reflective Prompt
Clarke’s study (2002) found that one of the characteristics common to effective teachers of numeracy was the ability to use teachable moments as they occurred and to make connections to mathematical ideas from previous lessons or experiences.
How do you recognise when teachable moments occur?
What numeracy opportunities do you create in your lessons that enable students to make mathematical connections?
Reflective Prompt
Clarke’s study (2002) found that one of the characteristics common to effective teachers of numeracy was the ability to use teachable moments as they occurred and to make connections to mathematical ideas from previous lessons or experiences.
How do you recognise when teachable moments occur?
What numeracy opportunities do you create in your lessons that enable students to make mathematical connections?
Developing teachers’ capacity to teach numeracy
The review of relevant literature revealed that a number of researchers are working with teachers to help them reflect upon and investigate their approaches to teaching numeracy (e.g., Bennison, 2016; Farragher, Poore, & Gaffney, 2014; Goos, Geiger, & Dole, 2011; Liljedahl, 2015; Liljedahl, 2011).
For example, Liljedahl (2015) worked with a group of mathematics teachers on developing numeracy tasks. The results indicated that the teachers’ experiences with designing these tasks, and pilot testing them in their own classrooms, propelled them to make changes in their own mathematics teaching practice.
Read the article by Peter Liljedahl (2015), Numeracy task design: a case of changing mathematics teaching practice.
Reflective Prompt
What motivated these teachers to change their numeracy practice?
Reflective Prompt
What motivated these teachers to change their numeracy practice?
Professor Peter Sullivan has led many projects promoting challenging tasks in teaching mathematics and relates these to developing students’ mathematical understanding in ways that support numeracy (Sullivan, 2011).
In the video clip below, Professor Peter Sullivan explores the analogy of an Easter egg hunt to explain how to promote challenging tasks.
Observe Professor Peter Sullivan talking about challenging and supporting tasks.
Reflective Prompt
How might you use Professor Peter Sullivan’s analogy in developing rich numeracy tasks?
Reflective Prompt
How might you use Professor Peter Sullivan’s analogy in developing rich numeracy tasks?
Effective teaching of numeracy in indigenous and remote contexts
Professor Robyn Jorgensen’s (2018) project, Celebrating success: Numeracy in remote Indigenous contexts, was carried out over 3 years with 39 schools ranging from primary to secondary and VET schools from around Australia.
Case studies of 35 schools focused on the strengths of the schools in promoting numeracy in remote regions. These case studies are located on the project website.
In the final report, published in April 2018, the key findings suggested there was no one unifying approach across the schools or the states; and the schools used multiple approaches from problem-solving inquiry to direct instruction. However, there were some common features between the schools. These were:
- Identifying the needs of the students and targeting teaching to meet these needs
- Having a clear vision of the school’s culture, and sharing this with the community
- Enabling staff and students to meet goals and to enact the vision
- Being explicit about the intent of learning and what is expected of the students
- Teaching in a culturally responsive way that bridged between home and school, and focused on the language in mathematics
- Having high expectations and prioritising learning in
mathematic - Helping students see a purpose for numeracy
Whilst the features identified by Professor Jorgensen relate to remote Indigenous contexts, the features relate more generally to good practice.
In particular, the focus on culturally responsive pedagogies and connections to local communities are relevant to urban indigenous communities in states such as Victoria.
Watch Professor Robyn Jorgensen talking about her project in the video below.
Reflective Prompt
What experiences do Indigenous children have that help them foster numeracy understandings?
How can we capitalise on the numerate behaviours Indigenous children have when they enter educational settings?
Reflective Prompt
What experiences do Indigenous children have that help them foster numeracy understandings?
How can we capitalise on the numerate behaviours Indigenous children have when they enter educational settings?
Numeracy in the early years
The learning which occurs in the early years is important, both in and of itself, as well in relation to future success” (Dockett, 1995, as cited in Perry, 2000, p. 4)
The contextual learning that occurs in many early childhood settings means that differences between the development of mathematics and numeracy can be small, suggesting that the contextual learning of mathematics and numeracy can go hand in hand (Perry, 2000).
Perry (2000) identified a number of fundamental principles underlying young children’s learning. Although generic in nature, the principles have synergies with practices and beliefs that underpin the development of numerate behaviours in young children.
The principles include reference to development occurring in a relatively orderly sequence, the recognition that children are active learners, who draw on direct physical and social experience and culturally transmitted knowledge to construct their own understandings of the world around them, and the importance of play and conversation.
Read Perry’s full report, ‘Early childhood numeracy’.
In a recent review of research into ‘Mathematics Education in the Early Years’, MacDonald, Goff, Dockett and Perry (2016) found that there were four key themes that emerged in canvassing the current research:
- Curriculum in early childhood mathematics education
- Assessment in early childhood mathematics education
Content of early childhood mathematics education- Contexts for early childhood mathematics education
Of the 61 articles cited for the period of 2012-2015, only three explicitly mentioned numeracy (Goff, Dockett & Perry, 2013; Papic, 2013; Smith, 2015) – authors were concerned primarily with early mathematics education.
Nevertheless, the review demonstrates that there is extensive Australasian research about early mathematics education, including environmental, human and socio-cultural contexts in which early childhood education occurs (e.g., Goff, et al., 2013; McDonald & Howell, 2012; Muir, 2012; Papic, 2013).
Much of this mathematics education research contributes to our understanding of how to develop numeracy in young children.
Recognition of prior to school experiences
As part of a wider project investigating how mathematics learning might be supported as children start school, Goff, et al. (2013) found that “numeracy might not be a key priority for schools as children make the transition from preschool to primary school” (p. 367).
An extensive body of literature, however, stresses the importance of recognising the prior to school numeracy experiences many young children bring to formal schooling (e.g., Gervasoni & Perry, 2013; Knaus, 2013; MacDonald, 2018; Worthington, 2018).
Young children often bring a great deal of mathematical knowledge and dispositions for learning mathematics to formal schooling, with much of it having been learned from everyday experiences (Perry, Dockett, & Harley, 2012).
A review of the research noted the predictive power of mathematical knowledge at school entry for later mathematical achievement (MacDonald, 2018).
Worthington (2018) noted that teachers are often not aware of children’s mathematical ‘funds of knowledge’ (Moll, Amanti, Neff, & Gonzalez, 1992) or the rich cultural knowledge they have developed. She describes a number of examples which demonstrate how children’s home cultural experiences are manifested in pretend-play and other child-initiated activities in early educational settings.
For example, Worthington documented the case of ‘Shereen’ whose funds of knowledge and cultural home experiences were linked with buying, preparing, ordering and eating food, which
All of Shereen’s pretend-play narratives were centred on food, either shopping for food or playing cafes in which she took orders for food, informed customers of items available and their cost and even admonished those who failed to eat everything.
Reflective Prompt
As a teacher, what can you do to discover the ‘funds of knowledge’ that your early learners bring to formal schooling?
As a parent, how can you ensure that your child’s teacher is aware of their ‘funds of knowledge’?
Reflective Prompt
As a teacher, what can you do to discover the ‘funds of knowledge’ that your early learners bring to formal schooling?
As a parent, how can you ensure that your child’s teacher is aware of their ‘funds of knowledge’?
The importance of play
Play is regarded as a significant feature of effective early years’ pedagogy and has a focus on how children learn rather than what children learn (Tucker, 2014).
Play can take many forms, and may include ‘free-flow play’ (Bruce, 1991), where play is freely chosen by the child and is characterised by:
- Child-initiated activity in a meaningful context
- Child controlled and ownership of the activity by imagining, making decisions and predictions
- Experimenting with strategies and taking risks in a safe context
- Showing curiosity
- Seeking pleasure from the essence of the activity
“Play is the work of the child” [Maria Montessori]
According to Fisher (2010), to fully support mathematical and/or numeracy development, playful activity requires adult involvement at some level; a balance of practitioner-led, practitioner-initiated and child-initiated activity is desirable.
Others (e.g., Worthington, 2018) warn against the ‘pedagogization of play’ that is ‘planned’ or ‘structured’ to meet curriculum targets (Worthington, 2018, p. 254), resulting in play being marginalised and misunderstood. She argues that spontaneous and sustained social pretend-play can create a rich social-ecocultural niche in early childhood.
This spontaneous play often occurs in contexts that are meaningful to young children, thus providing an ideal opportunity to promote numerate behaviour.
The Victorian Early Years Learning and Development Framework (VEYLDF) (DET, 2016, p. 14) establishes that play is essential to stimulate and integrate a wide range of children’s intellectual, physical, social and creative abilities. The framework distinguishes between integrated child-directed play and learning, guided play and learning, and adult-led learning, but acknowledges that all are effective in advancing children’s knowledge.
Play is explicitly referred to in the VEYLDF Practice Principle 7: Integrated Teaching and Learning approaches where it is named as an essential element in early childhood learning and development. Furthermore play has been shown to:
- Allow for the expression of personality and uniqueness
- Enhance dispositions such as curiosity and creativity
- Enable children to make connections between prior experiences and new learning
- Assist children to develop relationships and concepts
- Stimulate a sense of wellbeing. (DEEWR, 2009)
According to MacDonald (2018), play contexts provide opportunities for children’s spontaneous invention of their own mathematical strategies where they will often use their lived experiences to inform the play, resulting in solving problems presented in the play.
To learn more about practical examples of the teaching of numeracy through play, see the Birth to Level 2 sections of the Numeracy Focus Areas.
Reflective Prompt
Why are everyday behaviours such as setting the table and playing in the sandpit provided as examples of numerate behaviour? What mathematics underpins such behaviours?
What do you see as the difference between structured and spontaneous play?
To what extent do you think an adult might participate in children’s play?
Reflective Prompt
Why are everyday behaviours such as setting the table and playing in the sandpit provided as examples of numerate behaviour? What mathematics underpins such behaviours?
What do you see as the difference between structured and spontaneous play?
To what extent do you think an adult might participate in children’s play?
At home with numeracy
“Even though it looked like you were just playing a game, you could see the benefit of the numeracy and the maths skills in it” (Muir, 2018, p. 173)
There is
This involvement
In terms of the relevance for early childhood numeracy development, the literature reviewed showed that parents remain largely uninformed about contemporary mathematics practices and how they can assist in developing their child’s numeracy at home (e.g., Muir, 2009; Muir, 2012; Pritchard, 2004).
There are a number of initiatives and programs that have been documented in the literature that have been shown to build an increased understanding of contemporary mathematics classroom practices (Muir, 2018).
Sheldon and Epstein (2005) found, for example, that a number of involvement activities that were effective included evening workshops, involving both parents and children, and provision of teacher-designed interactive homework and mathematics materials for families to use at home.
Other research has reported on the use of ‘
Reflective Prompt
Read the article ‘Numeracy at home: Involving parents in mathematics education’.
What was the impact of the intervention on parents’ understanding of contemporary mathematics practices?
As an early childhood educator, what could you do to help parents develop their child’s numeracy?
As a parent, what could you do to develop your child’s numeracy?
Reflective Prompt
Read the article ‘Numeracy at home: Involving parents in mathematics education’.
What was the impact of the intervention on parents’ understanding of contemporary mathematics practices?
As an early childhood educator, what could you do to help parents develop their child’s numeracy?
As a parent, what could you do to develop your child’s numeracy?
References
Adoniou, M. & Qing, Y. (2014). Language, Mathematics and English Language Learners. Australian Mathematics Teacher, 70(3), 3-13.
Australian Curriculum, Assessment and Reporting Authority. (2017). Australian Curriculum: Mathematics. Retrieved from https://www.australiancurriculum.edu.au/resources/mathematics-proficiencies/
Askew, M., Rhodes, V., Brown, M., Wiliam, D., & Johnson, D. (1997). Effective teachers of numeracy: Final report. London, UK: King’s College London School of Education.
Bennison, A. (2016). Teacher identity as an embedder-of-numeracy: Identifying ways to support teachers to promote numeracy learning across the curriculum. St Lucia, QLD: University of Queensland.
Bennison, A. (2014). Understanding identity as a teacher of numeracy in history: A sociocultural approach. Paper presented at the joint International Conference Australian Association for Educational Research [AARE] and New Zealand Association for Research Education [NZARE]. Brisbane, QLD: AARE-NZARE.
Bragg, L. A. & Herbert, E. (2017). A “true” story about mathematical reasoning made easy. Australian Primary Mathematics Classroom, 22(4), 3-8.
Bragg, L. A., Loong, E. Y.-K., Widjaja, W., Vale, C., & Herbert, S. (2015). Promoting reasoning through the Magic V task. Australian Primary Mathematics Classroom, 20(2), 10-14.
Clark, R. E., Kirschner, P. A., & Sweller, J. (2012). Putting students on the path to learning: The case for fully guided instruction. American Educator, Spring, 6-11.
Clarke, D. M. (2005). Written algorithms in the primary years: Undoing the ‘good work’?. In M. Coupland, J. Anderson, T. Spencer (Eds.) Making mathematics vital: Proceedings of the twentieth biennial conference of the Australian Association of Mathematics Teachers [AAMT], pp. 93-98. Adelaide, Australia: AAMT.
Clarke, D., Cheeseman, J., Gervasoni, A., Gronn, D., Horne, D., McDonough, A., Montgomery, P., Roche, A., Sullivan, P., Clarke, B., & Rowley, G. (2002). Early numeracy research project final report. Melbourne, VIC: Australian Catholic University.
Clarke, D. M., Clarke, D. J., & Sullivan, P. (2012). Reasoning in the Australian Curriculum: Understanding its meaning and using the relevant language. Australian Primary Mathematics Classroom, 17(3), 28-32.
Cockcroft, W. (1982). Mathematics counts: report of the Committee of Inquiry into the teaching of mathematics in schools. London: HMSO.
Cooper, C., Dole, S., Geiger, V., & Goos, M. (2012). Numeracy in society and environment. The Australian Mathematics Teacher, 68(1), 16-20.
Crowther, G. (1959). 15 to 18: A report of the Central Advisory Council for Education (England). London, UK: HMSO.
Department of Education, Employment and Workplace Relations for the Council of Australian Governments. [DEEWR] (2009). Belonging, being and becoming: The Early Years Learning Framework for Australia, Canberra: Australian Government.
Department of Employment, Education, Training and Youth Affairs. [DEETYA] (1997). Numeracy = Everyone’s Business: The report of the numeracy education strategy development conference. Canberra: Australian Association of Mathematics Teachers.
Department of Education and Training. (2016). Victorian Early Years Learning and Development Framework. Melbourne, VIC.
Faragher, R., Poore, M., & Gaffney, M. (2014). Networking Numeracy Development. In M. Gaffney, & R. Faragher (Eds.), Leading Improvements in Student Numeracy (1 ed., pp. 113-126). Camberwell, VIC: Australian Council of Educational Research [ACER] Press.
Geiger, V., Goos, M., & Forgasz, H. (2015). A rich interpretation of numeracy for the 21st century: a survey of the state of the field. ZDM Mathematics Education, 47, 531–548.
Gervasoni, A., & Perry, B. (2013). Children’s mathematical knowledge prior to starting school. In V. Steinle, L. Ball, & C. Bardini (Eds.), MERGA 2013: Mathematics education: Yesterday, today and tomorrow: Proceedings of the Mathematics Education Research Group of Australasia 2013 conference, pp. 338-345, Mathematics Education Research Group of Australasia Inc., Melbourne, VIC: MERGA.
Goff, W., Dockett, S., & Perry, R. (2013). Principals’ views on the importance of numeracy as children start primary school. In V. Steinle, L. Ball, & C. Bardini (Eds.), MERGA 2013: Mathematics education: Yesterday, today and tomorrow: Proceedings of the Mathematics Education Research Group of Australasia 2013 conference, pp. 362-368, Mathematics Education Research Group of Australasia Inc., Melbourne, VIC: MERGA.
Goos, M., Geiger, V., & Dole, S. (2012). Changing teacher practice through a rich model of numeracy across the curriculum. In Gangnae-Myeon, Cheongwon-Gun, Chungcheongbuk-Do (Eds.), 12th International Congress of Mathematical Education, Seoul, The Republic of Korea, pp. 4329-4337, Korea National University, Republic of Korea: International Congress on Mathematical Education [ICME].
Goos, M., Geiger, V., & Dole, S. (2011) Teachers’ personal conceptions of numeracy 2011. In B. Ubuz (Ed.). Proceedings of the 35th Conference of the International Group for the Psychology of Mathematics Education [PME], Vol. 2, pp. 457- 464. Ankara, Turkey: PME.
Goos, M., Geiger, V., Dole, S., Forgasz, H., & Bennison, A. (2019). Numeracy across the curriculum: Research-based strategies for enhancing teaching and learning. Sydney: Allen & Unwin.
Goos, M., & Jolly, L. (2004). Building partnerships with families and communities to support children’s numeracy learning. In I. Putt, R. Faragher & M. McLean (Eds.), Mathematics education for the third millennium: Towards 2010. Proceedings of the 27th annual conference of the Mathematics Education Research Group of Australasia [MERGA], pp. 279-286. Townsville, QLD: MERGA.
Gould, P. (2016). The will, the skill and the understanding. Scan, 35(2), 16-19.
Groves, S., Mousley, J., & Forgasz, H. (2006). Primary numeracy: A mapping, review and analysis of Australian research in numeracy learning at the primary school level. Canberra: Department of Education, Science and Training.
Heirdsfield, A., Shelley, D., & Beswick, K. (2007). Instruction to support mental computation development in young children of diverse ability. In P. Jeffery, P. L., (Ed.) Proceedings of the Australian Association for Research in Education Conference [AARE]. Adelaide, Australia: AARE.
Hogan, J. (2000). Numeracy – Across the curriculum? The Australian Mathematics Teacher, 56 (3), 17-20.
Howden, H. (1989). Teaching number sense. Arithmetic Teacher, 36(6), 6-11.
Hurst, C. (2018). A tale of two kiddies: A Dickensian slant on multiplicative thinking. Australian Primary Mathematics Classroom, 23(1), 31-36.
Johnston, B. (1994). Critical Numeracy. Fine Print, 16(4), 32-36.
Jorgensen, R. (2018). Celebrating Success: Numeracy in Remote Indigenous Contexts: Final Report. Canberra: University of Canberra.
Knaus, M. (2013). Maths is all around you: Developing mathematical concepts in the early years. Albert Park, VIC: Teaching Solutions.
Liljedahl, P. (2015). Numeracy task design: a case of changing mathematics teaching practice. ZDM Mathematics Education, 47, 625–637.
Liljedahl, P. (2010). Noticing rapid and profound mathematics teacher change. Journal of Mathematics Teacher Education, 13(5), 411-423.
Loong, E., Vale, C., Bragg, L. A. & Herbert, S. (2013). Primary school teachers’ perceptions of mathematical reasoning, In V. Steinle, L. Ball & C. Bardini, (Eds.), MERGA 2013: Mathematics education: Yesterday, today and tomorrow: Proceedings of the Mathematics Education Research Group of Australasia 2013 conference, pp. 466-473, Mathematics Education Research Group of Australasia Inc., Melbourne, VIC: MERGA.
MacDonald, A. (2018). Mathematics in early childhood education. Melbourne, VIC: Oxford University Press.
MacDonald, A., Goff, W., Dockett, S., & Perry, B. (2016). Mathematics education in the early years. In K. Makar, S. Dole, J. Visnovska, M. Goos, A. Bennison, & K. Fry (Eds.), Research in mathematics education in Australasia 2012 – 2015, pp. 165-186. Singapore: Springer.
McIntosh, A., Reys, R., & Reys,B. (1992). A proposed framework for examining basic number sense. For the Learning of Mathematics, 12(3), 2- 9.
Moll, L. C., Amanti, C., Neff, D., & Gonzalez, N. (1992). Funds of knowledge for teaching: Using a qualitative approach to connect homes and classrooms. Theory into Practice, 31(2), 132-141.
Morony, W. & Brinkworth, P. (2003). Springboards into numeracy: Proceedings of the National Numeracy Conference 4-5 October 2002. Adelaide, SA: Australian Association of Mathematics Teachers.
Muir, T. (2018). Using mathematics to forge connections between home and school. In V. Kinnear, M.Y. Lai, & T. Muir (Eds.), Forging connections in early mathematics teaching and learning, pp. 173-190. Singapore: Springer.
Muir, T. (2012) It’s in the Bag: Parental Involvement in a Numeracy At-Home Program. Australasian Journal of Early Childhood, 37(2), 27-33.
Muir, T. (2009). At home with numeracy: Empowering parents to be active participants in their child’s numeracy development. In R. Hunter, B. Bicknell, & T. Burgess (Eds.), Crossing divides. Proceedings of the 32nd annual conference of the Mathematics Education Research Group of Australasia [MERGA], pp. 395-402. Wellington, NZ: MERGA.
O’Donoghue, J. (2002). Numeracy and mathematics. Irish Mathematical Society Bulletin, 48, 47-55.
OECD (Organisation for Economic Co-operation and Development). (2016). PISA 2015: Assessment and analytical framework: Science, reading, mathematics, and financial literacy. Paris: OECD.
Orman, S. A. (2000). Mathematics backpacks: Making the home-school connection. In D. Edge (Ed.), Involving families in mathematics education, pp. 51-53. Reston, VA: National Council of Teachers of Mathematics.
Perry, R., Dockett, S., & Harley, E. (2012). The Early Years Learning Framework for Australia and the Australian Curriculum: Mathematics-Linking educators’ practice through pedagogical inquiry questions. In D. S. D. Siemon (Ed.), Engaging the Australian Curriculum Mathematics: Perspectives from the field, (1 ed.), pp. 153-174. Australia: Mathematics Education Research Group of Australasia.
Perso, T. (2011). Assessing numeracy and NAPLAN. The Australian Mathematics Teacher, 67(4), 32-35.
Peters, C., Geiger, V., Goos, M., & Dole, S. (2012). Numeracy in health and physical education. The Australian Mathematics Teacher, 68(1), 21-27.
Pritchard, R. (2004). Investigating parental attitudes and beliefs in mathematics education. In I. Putt, R. Faragher, & M. McLean (Eds.), Mathematics education for the third millennium: Towards 2010. Proceedings of the 27th annual conference of the Mathematics Education Research Group of Australasia [MERGA], pp. 478-485. Townsville, QLD: MERGA.
Researching Numeracy Project Team. (2004). Researching numeracy teaching approaches in primary schools. Australian Primary Mathematics Classroom, 9(4), 27-29.
Reys, B., McIntosh, A., Reys, R. & Hope, J. (1997). Number sense: Simple effective number sense experiences. Palo Alto, CA, USA: Dale Seymour Publications.
Sawatzki, C. (2017). Lessons in financial literacy task design: Authentic, imaginable, useful. Mathematics Education Research Journal, 29(1), 25-43. DOI 10.1007/s13394-016-0184-0
Sellars, M. (2017). Numeracy across the curriculum: A pathway to critical thinking. International Journal of Innovation, Creativity and Change, 3(2), 75-83.
Sellars, M. (Ed.) (2018). Numeracy in authentic contexts: Making meaning across the curriculum. Singapore: Springer.
Sheldon, S. B., & Epstein, J. L. (2005). Involvement counts: Family and community partnerships and mathematics achievement. Journal of Educational Research, 98(4), 196-206.
Sullivan P. (2011). Teaching Mathematics: Using research-informed strategies. Camberwell, VIC: Australian Council of Educational Research [ACER] Press.
Turner, R. (2011). Identifying cognitive processes important to mathematics learning but often overlooked. The Australian Mathematics Teacher, 67(2), 22-26.
Tucker, K. (2014). Mathematics through play in the early years, 3rd Edition. London, UK: Sage Publications.
Vale, C., Bragg, L. A., Widjaja, W., Herbert, S., & Loong, E. Y.-K. (2017). Children’s mathematical reasoning: Opportunities for developing understanding and creative thinking. Australian Primary Mathematics Classroom, 22(1), 3-8.
Victorian Curriculum and Assessment Authority. (VCAA). (2017). Victorian Curriculum: Mathematics. Retrieved from http://victoriancurriculum.vcaa.vic.edu.au/mathematics/curriculum/f-10
Victorian Curriculum and Assessment Authority. (VCAA). (2017). Numeracy Learning Progressions mapped to Victorian Curriculum F–10: Mathematics. Melbourne, VIC: Author.
Watson, J. (2009). Critical numeracy. Retrieved from http://tas-education.org/numeracy/critical_numeracy/critical_numeracy.htm
Westwood, P. (2011). The problem with problems: Potential difficulties in implementing problem-based learning as the core method in primary school mathematics. Australian Journal of Learning Difficulties, 16(1), 5-18.
Willis, K., Geiger, V., Goos, M., & Dole, S. (2012). Numeracy for what’s in the news and building an expressway. The Australian Mathematics Teacher, 68(1), 9-15.