Setting Goals
Clear learning intentions and goals clarify what success looks like
Numeracy Focus: Understanding, estimating, and using measurement
Learning area: Victorian Curriculum: Mathematics
In this podcast, Jen Bowden discusses the importance of having discussions with students to ensure they set goals they understand and are able to achieve. Through these discussions, teachers can use key language, which are purposeful for students and can help them build behaviour, i.e., they engage actively with their learning goal, they participate in peer and self-assessment and they can self-monitor their progress and development.
Teachers and students can co-design visual representations, displays or ‘I can’ statements to gauge what success looks like in the classroom for individuals. It is important that students identify the goals they achieved to plan the ‘where to next’ phase in their learning.
Jen Bowden explains that knowing students’ behaviours, actions, and learning is imperative. Goals are based on assessment that can be conducted through conferences or observations across all domains of learning. She offers an example of how a student can improve their numeracy skills through physical education.
Further, Jen explains how goals are embedded in classroom practice and adaptable across the curriculum into specialist areas or the students’ homes.
Setting Goals Podcast
Listen to Jen Bowden from the Mathematical Association of Victoria explain how to link numeracy goals to assessment to challenge all students in the classroom
Reflective Prompt
Ask yourself the questions we asked Jen:
- What are the key steps in setting effective numeracy goals?
- How can you ensure that the numeracy learning goals you set are clearly communicated to the students?
- How can you set realistic goals to challenge all students in your classroom?
- How do you encourage students to engage actively in planning goals for their numeracy learning?
- Please explain why it is necessary to link numeracy goals to assessment
Reflective Prompt
- What are the key steps in setting effective numeracy goals?
- How can you ensure that the numeracy learning goals you set are clearly communicated to the students?
- How can you set realistic goals to challenge all students in your classroom?
- How do you encourage students to engage actively in planning goals for their numeracy learning?
- Please explain why it is necessary to link numeracy goals to assessment
- Based on assessed student needs
- Goals are presented clearly so students know what they are intended to learn
- Can focus on surface and/or deep learning
- Challenges students relative to their current mastery of the topic
- Links to explicit assessment criteria
Further resources
Structuring Lessons
A lesson structure maps teaching and learning that occurs in class
Numeracy Focus: Developing number sense; Using proportional reasoning; Understanding, estimating, and using measurement; Exploring chance and data
Learning area: Languages: German, Victorian Curriculum: Mathematics
The video, Numeracy Across the Curriculum, explores how to incorporate numeracy in a German language program. Vicki Dunn explains the steps students take to plan for a class project, which entails preparing a trip overseas to Germany. Although this is for a year 9 class, it is suitable for various ages (i.e. grades 5-8). See the link to the Mathematics and Geography Travel Unit below.
Students in Vicki’s class were able to explore numeracy through:
- money exchange rates namely, converting between Australian Dollars and the Euro using arithmetic operations
- temperature i.e. exploring weather patterns using statistical data
- location i.e. map coordinates and investigating longitude and latitude
- time: i.e., exploring different time zones
- statistics: i.e., reading graphs and timetables
The students use a variety of problem-solving strategies to make decisions and justify their answers.
When structuring a numeracy lesson, it is important to have a clear plan of the sequence of activities, assessment strategies, and the amount of time dedicated to a topic. This plan ensures that the lessons within a unit are stimulating and allow students to make connections in their learning. To encourage student success, the planned lessons should include clearly stated learning goals, ample time to explore concepts, time for reflection on learning, and provision of timely feedback.
The pedagogical model can provide a structure for inquiry lessons based on a constructivist approach to learning.
The five domains of the pedagogical model are:
Engage: This is the first step and should provide a ‘hook’ to engage students in a new skill, idea or concept. This hook should be a problem or question that is relevant to the students and has the potential to activate prior knowledge.
Explore: This step provides hands-on activities for students to investigate a mathematics concept. Students work together to share their thinking and ask questions. The teacher observes and listens and asks probing questions.
Explain: This is the step where the teacher uses the students’ thinking to direct the focus of the lesson to the intended learning.
Elaborate: This step is where the students are given the opportunity to apply the concept and to move to generalisations and abstractions.
Evaluate: This can happen formatively throughout the lessons but there should also be an opportunity to sum up learning at the end of the lessons.
You may not need to use all these steps in one period as the lesson can extend over several periods.
Listen to classroom teacher Vicki Dunn as she explains how she structured lessons and embedded numeracy into her German language studies
Reflective Prompt
What similarities and differences did you notice in Vicki Dunn’s account of her German class compared with how you structure a lesson to support numeracy?
Consider what strategies you employ in your teaching to help students make clear links between the learning goals and assessment tasks.
Reflective Prompt
Consider what strategies you employ in your teaching to help students make clear links between the learning goals and assessment tasks.
- Clear expectations
- Sequencing and linking learning
- Clear instructions
- Clear transitions
- Scaffolding
- Questioning/feedback
- Formative assessment
- Exit cards
Further resources
Marcus Garrett, Australian Mathematical Sciences Institute Schools Outreach Officer, provides insights into how to plan and deliver effective mathematics lessons in his blog. Read Marcus’ blog to see ‘What makes for a ‘good’ maths lesson?’
Australian Curriculum Lessons have developed a unit of work integrating geography and mathematics designed around students planning an overseas holiday. Explore the Mathematics and Geography Travel Unit
Explicit Teaching
Explicit teaching practices show students what to do and how to do it
Numeracy Focus: Developing number sense
Learning area: Victorian Curriculum: Mathematics
Explicit teaching is not prescriptive teaching of processes and algorithms. Explicit teaching of numeracy involves the teacher modelling and demonstrating mathematical concepts using materials, representations, problems, and open-ended questions to help students’ exploration of mathematical ideas that underpin numeracy.
In this video Professor Jo Boaler demonstrates five different mental calculation strategies to solve the equation 18 x 5. She uses representations, based on the area model, to make visual connections between the different strategies and to make explicit the underlying mathematical principles.
By modelling the mathematical ideas explicitly, students can apply their new knowledge to develop the intended numeracy skills in a lesson.
Students should be given ample time to engage with the new learning and to practise, applying their new skills. The teacher provides students with valuable and immediate feedback and monitors their progress.
Notice in the video how Professor Jo Boaler teaches multiplication through visual representations that help to make the mathematical ideas explicit and build students’ number sense
Reflective Prompt
How might you go about using visual representations to foster students understanding of number sense?
How could you use technology to foster understanding of number sense?
Reflective Prompt
How could you use technology to foster understanding of number sense?
- Shared learning intentions
- Relevant content and activities
- New content is explicitly introduced and explored
- Teacher models application of knowledge and skills
- Worked examples support independent practice
- Practice and feedback loops uncover and address misunderstandings
Further resources
Worked Examples
Worked examples demonstrate the steps required to complete a task or solve a problem
Numeracy Focus: Developing number sense; Using proportional reasoning; Understanding, estimating, and using measurement
Learning area: Design Technologies, Victorian Curriculum: Mathematics, Health and Physical Education
In this activity, students work in small groups and create a plan to scale a recipe. After watching a worked example demonstrated by the teacher using the basic recipe for 12 cakes, students can transfer the skills and knowledge modelled in the examples to work on the goal of the task. The goal is for students to adjust recipes based on the set of cards given to them.
They each have the basic recipe cards and decide what happens to the recipe for 24 cakes, 6 cakes and 36 cakes instead of the 12 cakes. Some information is missing from the ingredients list which students need to find.
Next, they use arrow cards to show relationships between the different groups of cards such as x 6 or ÷ 6.
When introducing each worked example ensure that students are challenged. For example, omit a few steps so that students can use problem solving and self-questioning to find answers.
Click on the image above to try this resource from NRICH, which explores worked examples through cooking. In this resource, numeracy is integrated with food technology to help students use proportional reasoning to calculate scaled recipes
Reflective Prompt
Children and young people can be thoroughly engaged through lessons that involve cooking, specifically when it is reflective of their backgrounds and life worlds.
Do you believe the ideas presented in Changing Recipes would work with your own students or children to support fluency in proportional reasoning?
Make a video of the worked examples. Are the resources and instructions sufficiently explanatory to unpack the skill being learnt and yet still maintain a level of challenge?
Reflective Prompt
Do you believe the ideas presented in Changing Recipes would work with your own students or children to support fluency in proportional reasoning?
Make a video of the worked examples. Are the resources and instructions sufficiently explanatory to unpack the skill being learnt and yet still maintain a level of challenge?
- Teacher clarifies the learning objective, then demonstrates what students need to do to acquire new knowledge and master new skills
- Teacher presents steps required to arrive at the solution so students’ cognitive load is reduced and they can focus on the process
- Students practice independently using the worked example as a model
Further resources
Supporting the Australian Mathematics Project includes resource packages for teachers of Level 5 to 9 students. The resources are designed to aid teachers and students in the implementation of the mathematics curriculum. The materials provide worked examples, followed by student practice. Explore the Australian Mathematical Sciences Institute
The Improving Mathematics Education in Schools (TIMES) Project offers modules demonstrating how numeracy practice can be spaced during mathematics lessons. The module materials include worked examples in progressive steps to support students’ independent practice. Visit the Australian Mathematical Sciences Institute
Collaborative Learning
Students work in small groups and everyone contributes to learning tasks
Numeracy Focus: Exploring patterns and relationships; Using proportional reasoning
Learning area: The Arts: Music, Victorian Curriculum: Mathematics
Collaborative learning to promote numeracy involves students working together on a group goal to solve a problem or create a product. Collaboration involves each student being individually accountable as well as the group being collectively accountable.
Collaborative learning requires students to engage dialogically with each other and promotes critical thinking and mathematical understanding in meaningful ways.
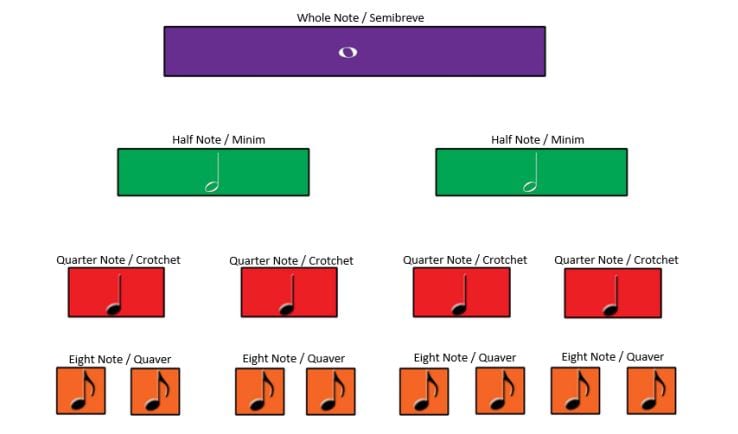
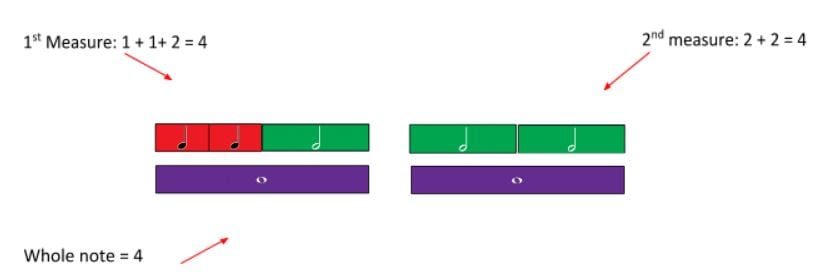
In this example of fostering numeracy through music, students collaborate to create rhythmic patterns through musical arrangements. Students calculate the beats as fractions of a whole (the musical measure. Click here for Note names and values resource). The students work towards a common goal in creating rhythms that when combined are pleasant to listen to.
- participate actively
- negotiate roles and responsibilities
- contribute to the task
- receive valuable feedback from their group and the teacher
To help students add various beats to equal a whole note, invite them to use a rhythm tree which is made with the fraction music cards. Students will notice that the rhythm tree resembles the familiar fraction wall. As shown, the shape and colour of the note indicates the length or duration.
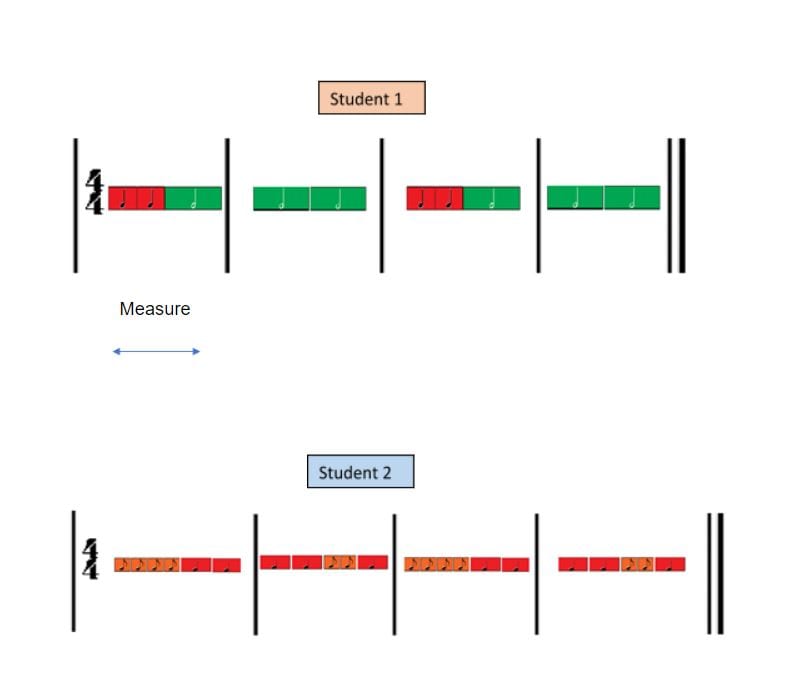
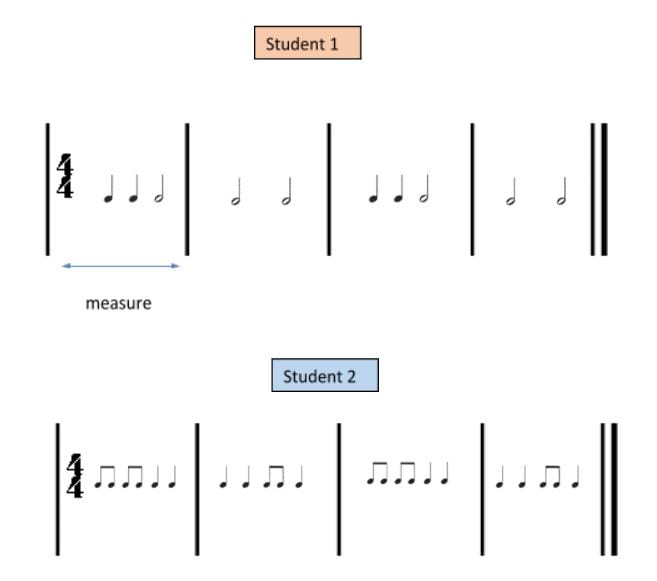
Student 1 clap pattern
Student 2 clap pattern
Students 1 and 2 clap pattern
Examine this music lesson plan and listen to the students collaborating as they clap their rhythms and explore music through numeracy
Reflective Prompt
Music is extremely motivating for children and young people. How might you introduce popular music with students to foster problem solving through collaboration?
How might you plan a lesson for students to create their own rhythms that helps promote understanding of patterns and relationships?
Reflective Prompt
How might you plan a lesson for students to create their own rhythms that helps promote understanding of patterns and relationships?
- Students work together to apply previously acquired knowledge
- Students cooperatively solve problems using previously acquired knowledge and skills
- Students work in groups that foster peer learning
- Groups of students compete against each other
Further resources
Multiple Exposures
Students are given multiple opportunities to encounter, engage with, and elaborate on new knowledge and skills
Numeracy Focus: Exploring patterns and relationships; Understanding and using geometric properties and spatial reasoning; Understanding, estimating, and using measurement
Learning area: Victorian Curriculum: Mathematics, The Arts: Dance
Multiple exposures give students the opportunity to engage with new knowledge and skills in a variety of ways. Students can attain knowledge with deep understanding as they explore content through various means and situations and learn to adjust their new skills when applying them to different contexts.
In this video Malke Rosenfeld demonstrates how students can explore time, patterns, and geometry through dance. As the students create their own percussive dance pattern, they develop skills in spatial awareness, spatial language, symmetry, angles, patterns and problem solving.
Students gain new insights, adapt previously learnt skills and apply them to new areas. For example:
- the steps are performed in unison, hence they are congruent
- symmetry is used in dance to develop stage performance i.e., rotational and reflection symmetry
- students within pairs to construct steps using repeating patterns and a four-beat structure; These beats are combined with other groups to make 8 beats and can follow a binary pattern e.g., ABAB
- students use counts to keep in time with the music
- students use angles when rotating i.e. 90°, 180°, 270° or 360°
This activity demonstrates how students can apply mathematics in the arts through dance and engage in hands-on learning. Students think creatively through movement and the environment around them.
Watch the video of a dancer and teacher Malke Rosenfeld as she explains how she uses percussive dance to teach geometry concepts
Reflective Prompt
How might you use the Multiple Exposures resource in your setting to promote students’ numeracy?
Reflective Prompt
How might you use the Multiple Exposures resource in your setting to promote students’ numeracy?
- Students have time to practice what they have learnt
- Timely feedback provides opportunities for immediate correction and improvement
Further resources
Questioning
Questioning engages students, stimulates interest and curiosity in the learning, and makes links to students’ lives
Numeracy Focus: Developing number sense; Understanding, estimating, and using measurement
Learning area: Victorian Curriculum: Mathematics
The task requires students to make a dark green Cuisenaire rod that is exactly three times larger than the original rod. In this experimental task, students use centimetre grid paper to help with calculations. The focus is not solely based on obtaining an answer, but rather it focuses on students’ explanation and thinking.
Anna uses finding out and clarifying questions, and scaffolding understanding questions and prompts to determine students’ understanding and challenge their thinking. She uses specialising and exemplifying questions as well as altering and verifying questions to steer students’ thinking towards a correct understanding of the problem and to make sense of how to calculate the volume and surface area of various prisms. For example, the teacher asked:
- What do you notice?
- What do you see happening?
- What do you mean by…?
- So, if you are saying that…
- Why? I am not clear about this…
- What is a layer?
- How is volume different from surface area? If one rod uses 6 cubes how many cubes would make this larger version?
Questions prompted by teachers need to have an overall purpose namely, they assist:
- students’ to reason and justify answers to demonstrate how they thought about a situation
- providing teachers with feedback on the knowledge that students poses
- students to revise concepts and key ideas
- teachers challenge new ways of thinking
- students to engage in reflection
- refocusing students’ attention to the learning goals and objectives of a lesson
Listen to how Anna Torres uses questions and prompts to help her students express their ideas and draw out their learning. Read more and access her task resource Youcubed here.
Reflective Prompt
Effective questioning and using prompts both challenge and test students’ understanding and challenge their thinking. How have you used a similar approach in your setting to promote students’ understanding of number sense and/or measurement?
What kinds of questions from the five categories will you ask students to support their numeracy fluency?
Reflective Prompt
What kinds of questions from the five categories will you ask students to support their numeracy fluency?
- Plan questions in advance for probing, extending, revising and reflecting
- Teachers use open questions
- Questions used as an immediate source of feedback to track progress/understanding
- Cold call and strategic sampling are commonly used questioning strategies
Further resources
This NRich resource explains the use of questions to stimulate mathematical thinking. Read more about using questioning to stimulate mathematical thinking
This resource is a three page information sheet providing strategies and advice about effective questioning. Explore this resource on effective questioning
The W questions: Questions that start with when, why, where or what (and other similar W words) demand reasoning and explanations. How and if are ‘honorary’ W question starters. Delve into the Australian Association of Mathematics Teachers: Top Drawer
Feedback
Feedback informs a student and/or teacher about the student’s performance relative to learning goals
Numeracy Focus: Developing number sense
Learning area: Victorian Curriculum: Mathematics
According to Dylan Wiliam (2014), “Feedback involves a change of focus from what the teacher is putting into the process to what the learner is getting out of it.”
The feedback given to students can be in different forms; i.e., it can be verbalised, it may be a visual cue, or it can be written. Whatever the format, feedback should be positive, clear, and have specific links to the tasks at hand. It should inform students of any misconceptions they may develop and guide them towards thinking about ‘where to next’ in their learning.
John Hattie suggested a useful model: “Feed Up, Feed Back, Feed Forward”. This model relates to three questions:
- Feed Up: Where am I going (what are my learning intentions)?
- Feed Back: How am I going (what does the evidence tell me)?
- Feed Forward: Where to next (what learning activities should I do to make better progress)?
Used in this way, feedback becomes an ongoing tool that informs students of their success in reaching their learning goals.
The images above demonstrate Ben’s use of technology with students, to create and learn from digital portfolios. Access to the digital activities in an online portfolio means that Ben and fellow students view students’ work and offer constructive feedback.
In figure 1, we note one student (Joshua G) offers feedback on another student’s (Josh A) worded problem. Through reading the feedback offered to a peer, the teacher gains insights into Joshua G’s understanding of key elements in developing worded problems, namely an authentic, challenging context.
Note how Ben’s feedback to Sammy is positive and provides detail about her portfolio piece. For example, in the second image Ben provided the student with guidance on how to use language appropriately.
The feedback from both the teacher and the peer indicates what the student did well and how they can improve on the task and increase learning.
Figure 1. Image of peer to peer feedback on worded problem using technology
Figure 2. Image of teacher to student feedback on student’s video explanation
Reflective Prompt
How well do you think the feedback from Ben and his student covers the three questions in the Hattie model to promote understanding?
How might you use these three questions to help students develop peer feedback, using a digital resource such as Seesaw?
Reflective Prompt
How might you use these three questions to help students develop peer feedback, using a digital resource such as Seesaw?
- Precise, timely, specific, accurate and actionable
- Questioning and assessment is feedback on teaching practice
- Use student voice to enable student feedback about teaching
Further resources
The Department of Education and Training’s website to support feedback and reporting. Explore the information regarding feedback and reporting
A video of Stanford University Professor Jo Boaler detailing the importance of self and peer assessment. View the video
Laura Reynolds, an education consultant and curriculum writer, shares her useful tips for feedback. Examine the Giving student feedback: 20 tips for doing the right thing resource
In this video, staff at South Halls Head Primary School share their use of a range of feedback practices including learning goals and success criteria, self-assessment and peer-feedback, pre- and post-unit tests, and check-in activities to gauge student understanding. Delve into the AITSL Feedback Case Studies
The Australian Institute for Teaching and School Leadership (AITSL) have developed a short animated video describing what effective feedback is, how it can be used, and the potential impact on student learning. See the animated video on Feedback
Metacognitive Strategies
Metacognitive strategies teach students to think about their own thinking
Numeracy Focus: Developing number sense; Understanding and using geometric properties and spatial reasoning; Understanding, estimating, and using measurement
Learning area: The Arts: Media Arts, Victorian Curriculum: Mathematics
Metacognitive strategies enable students to think about their own thinking and development in unique ways. To help students reflect on their knowledge and experiences, provide them with opportunities to build their repertoire of problem solving strategies and engage them in open-ended tasks that allow them to reason, look back in their learning journey and think flexibly about numeracy.
Using pictures or photographs in mathematics is a great way to connect numeracy and the real world and encourages students to think about the mathematics involved and how it is applied to familiar contexts. Open-ended tasks allow for different interpretations which are driven by students varying abilities, knowledge and experiences.
Choose pictures that contain a numeracy focus to help students explore ideas and engage in creative thinking. In the chess board photo, some student responses are linked to determining the number of squares on the board. A student’s initial reaction may be to recognise the chessboard as an array i.e. they simply count 64 squares. It is important to ask students:
- How else can we think about this picture?
- How do you solve problems?
- What is the most effective way to go about this particular problem?
These prompts will allow students to think about the question in creative ways, which could lead them to interpret the image through algebraic thinking and reasoning. For example, students can connect smaller squares to make another square, which may lead them to make generalisations to determine the number of squares within any sized square. This could be achieved by simplifying the problem in that, the students start with a 2×2 square, then a 33 square and so forth, noting down the patterns they find in their results table.
As students respond to these questions, have them reflect on the problem solving processes they are using.
Dr Thelma Perso, former President of the Australian Association of Mathematics Teachers, lists five steps of problem solving that ask students to reflect on their thinking and use of strategies at each step:
- Clarify – what is the problem, what are we asked to find out?
- Choose – what strategies, tools or facts do we need to use?
- Use – students use the strategies, tools and facts
- Interpret – does the solution make sense in the context?
- Communicate – how can we best communicate the problem and its solution?
The photos in the PowerPoint (click on image) provide different contexts for exploring numeracy in everyday contexts, the first being a chess set. It poses the question: ‘What numeracy can you see?’ The images invite an imagination about possible problems for students to pose and consider.
What questions can you ask about this picture?
Reflective Prompt
What specific strategies can you use in your classroom to help students reflect on their thinking?
Reflective Prompt
What specific strategies can you use in your classroom to help students reflect on their thinking?
- Teaching problem solving
- Teaching study skills
- Promotes self-questioning
- Classroom discussion is an essential feature
- Uses concept mapping
Further resources
This video discusses the benefits of connecting classroom mathematics with the real world. Students engage in using creativity when thinking and reasoning. Watch this video particularly at the times (0-1:30 and 2:09-3:45)
Teach Magazine interview Australian Council for Educational Research (ACER) CEO Professor Geoff Masters AO to discuss why it is important that students can monitor their own learning. Hear the discussion about the importance of students monitoring their learning
This series of numeracy problems related to photographic images may be used to support students’ exploration of numeracy in their environment. Delve into the series of problem pictures
This example of an Irish initiative to encourage everyone in the community to develop maths eyes, and an appreciation for mathematics in everyday situations. Develop your ‘maths eyes’
Differentiated Teaching
Differentiated teaching are methods teachers use to extend the knowledge and skills of every student in every class, adjusting for content, process and product
Numeracy Focus: Developing number sense; Exploring chance and data
Learning area: Victorian Curriculum: Mathematics
Differentiating tasks and instruction ensures that all students have an opportunity to be enabled or extended in their learning and experience success within a lesson. Differentiated teaching occurs when teachers extend the knowledge and skills of every student in every class, regardless of their starting point. Students are appropriately challenged to build meaningful learning as teachers plan lessons that differentiate by content, process or outcome.
In Jodie’s approach to differentiated learning, the teachers have pre-assessed the range of needs in their classes and planned lessons accordingly. It is important for teachers to recognise and acknowledge what students already know to move forward and investigate what they need to learn next. Jodie’s lessons start with a warm-up task to engage the students. There is one learning outcome that all students are working towards, but the tasks are designed at a minimum of three levels. Students are asked to consider the skills for each task and decide which task will best suit their needs.
Watch as Jodie Parsons, an educational leader, differentiates her lesson to target all levels and encourages students to take ownership of learning through a numeracy investigation. Explore further in this Differentiation in maths resource from the Australian Institute for Teaching and School Leadership (AITSL).
Reflective Prompt
Jodie Parsons offers an inspiring account of ways she has redesigned her classroom practice. What can you take from her story to support the diverse capabilities of all learners in your classroom?
How are you supporting and fostering your EAL learners’ understanding of numeracy?
Reflective Prompt
Jodie Parsons offers an inspiring account of ways she has redesigned her classroom practice. What can you take from her story to support the diverse capabilities of all learners in your classroom?
How are you supporting and fostering your EAL learners’ understanding of numeracy?
- High quality, evidence based group instruction
- Regular supplemental instruction
- Individualised interventions
Further resources
The Australian Institute for Teaching and School Leaddership provides an example of a teacher discussing how students can explore algebraic problems at all levels of learning. See this video on teaching to the point of need
This Education Week animated video attempts to demystify differentiated teaching. View the video Differentiated instruction: It’s not as hard as you think